Surely that’s a typo…ergodicity!? No, it’s right! Ergodicity is a powerful concept in economic theory, investing, and personal finance.
Even if the name seems wild to you, the idea is simple—stick with me while I explain it. And then we’ll apply ergodicity to retirement planning and investing ideas.
By the end of this article, you’re going to be seeing ergodic systems and non-ergodic systems all over your life!
Ergodic, Non-Ergodic, and Russian Roulette
Ergodicity compares the time average of a system against the expected value of that system. Let’s explain those two terms: time average and expected value.
The time average asks, “If we did something a million, billion, trillion times…what would we expect the results to look like?” It needs to be a sufficiently long random sample.
The expected value asks, “By simply averaging probabilities, where would we expect the result to be?”
At first blush, you might think, “Those two are the same thing…right?” Right! Or, at least you’d be right if the system in question is ergodic.
I flip a coin a billion times, and I end up with a time average of 50/50 heads and tails. Alternatively, I could just use their known probabilities and surmise the expected value of 50/50.
In this case, the time average and the expected value are the same. Therefore, the system—coin flipping—is ergodic.
But let’s contrast coin flips against Russian Roulette. The expected value of Russian Roulette is optimistic. ~83% success and ~17% failure. But what happens if one “plays” a million times? Ahh! I think you’d agree that the time average of Russian Roulette is 100% failure.
When one fails in Russian Roulette, it is a devastating failure. To only look at the expected value of the system is too simple. The expected value is far different than the time average. Thus, Russian Roulette is non-ergodic.
Ergodicity –> Over and Over, Big & Small
Ergodicity rears its head in two circumstances. First, ergodicity matters when we do things over and over and over. And second, ergodicity matters when certain outcomes are meaningful while other outcomes are insignificant.
To further explain ergodicity, imagine this bet:
I have a 100-sided die.
I’ll roll the die and you pick a number. If it lands on any other number than your number, then you win $1000.
But if it lands on your number, then Mike Tyson punches you in the face and takes your money.

What a deal! You call 99 of your friends and you all come to take this bet. Sure enough, one of your friends loses. But the rest of you win a combined $99,000 and agree to pay for his medical bills (which may or may not be covered by the $99K…which is another crazy blog post waiting to happen).
The “ensemble average” is that you won! One individual loss doesn’t change that.
But would that result be the same if you had played 100 times by yourself? No! In that scenario, there’s a 63% chance that you’d eventually lose the roll, lose your money, and get punched in the face.
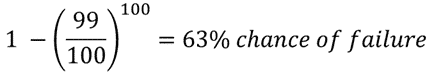
The expected value (you and all your friends) is different than the time average (you doing it 100x). This is not an ergodic process.
Revisiting Ergodicity & Coin Flips
We concluded earlier that coin flips are ergodic. The expected value of a single coin flip equals the time average results of many coin flips.
But let’s change the rules a bit. Imagine I promised you a 40% positive return on heads but a 30% loss on tails. You start with $100,000. Would you take this bet?
Again, let’s call up 100 of your friends. You each take the bet.
We can predict that half of you will end up with $140K (40% return) and half end up with $70K (a 30% loss). On average, you each have $105K. As a group, you’ll end up 5% higher than you started.
Sure enough, we can run this simulation a million times and that’s exactly what we see. Both the mean and median results of these simulation show a 5% profit. Taking the bet was smart.
But what if you took the bet 100 times? Same result?
Same for You?
To start, let’s look at two common snippets in the sequence of returns: one win followed by one loss, and one loss followed by one win.
Win then loss
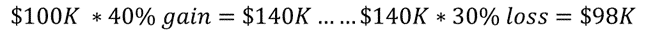
Loss then win
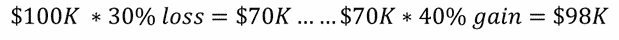
(You mathematicians will see the commutative property at play. The order of this multiplication didn’t matter.)
This result completely shifts our mindset.
When two people share a win/loss, they end up with $140K+$70K = $210K, or $105K each. They gain $5K. But when one person sequentially suffers a win/loss, she ends up with $98K, or a $2K loss.
What happens if you take this bet 100 times in a row? On average, you are going to lose money. Let’s look at a 50/50 heads/tails split.
Group 50/50:
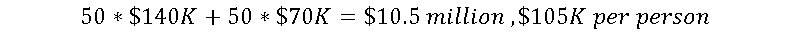
That’s a 5% profit.
You 50/50:
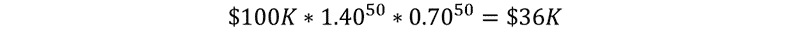
That’s a 64% loss
But you might “spike” a certain run where you get more heads than tails. What happens if the group gets 60 heads and 40 tails? What happens if you get 60 heads and 40 tails?
Group 60/40:
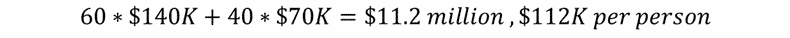
You 60/40:
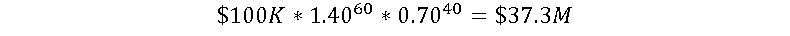
That’s…a big profit. $37.3 million.
I simulated the “you get 100 flips” case 100,000 times. As expected, the median result is a 64% loss. But the best result of the 100K simulations turns your $100K bet into $950 million dollars (68 heads, 32 tails).
This bet is non-ergodic. The expected value (100 friends scenario) is completely different than the time average (you 100x bets scenario).
But it’s also interesting that the distribution in the expected value case is tight (low risk, low reward) while the distribution in the time average case is extremely wide (high risk, potentially high reward).
EV is a profit, while time average is a loss. EV is low variance, while time average is high variance.
In case you can’t tell, ergodicity economics and subsequent economic theory is a serious field. There are big conversations taking place and serious money to be made (or lost).
But let’s focus a little closer to home: ergodicity and retirement.
Enjoying this article? Subscribe below to get new articles emailed straight to your inbox
Ergodicity and Retirement
In retirement planning, probability of success is often used as a figure of merit. I’ve used it here on the blog.
For example, the famous Trinity Study and 4% Rule cite a “95% chance of success,” where success is equivalent to “not running out of money before you die.”
Die with money? Success! Run out of money? Failure! This is an expected value metric—for 95% of all people, the 4% rule would have worked.
But a few problems in this thinking immediately arise and ergodicity is to blame.
Problem 1: Equal and Opposite?
The 5% of retirement fail cases are painful. Very painful. I would argue that the pain of failure in retirement is greater than the joy of success.
This is reminiscent of loss aversion, or the “tendency to prefer avoiding losses to acquiring equivalent gains.” The keyword in loss aversion is “equivalent.” People would rather avoid a $100 parking ticket than win a $100 lotto ticket. Those are equivalent. And yes, loss aversion is irrational.
But is failing in retirement equivalent-and-opposite to succeeding in retirement? I’d argue no. Failing in retirement is akin to a Russian Roulette loss. Devastating! And succeeding in retirement is a Russian Roulette win. It’s “expected.”
Problem 2: Expected Value & Risk Sharing
Let’s assume we all follow the 4% rule. And true to historical form, let’s assume that 95% of us have successful retirements, but 5% of us “fail” and run out of money.
In the previous examples—100 friends and Mike Tyson, or 100 friends and the 40% win/30% loss coin flip—we assumed that the group would share the risk and share the reward.
This guaranteed that we’d see profits, but eliminated our chance to win $950 million. This guaranteed that even if we did get face-punched by Mike Tyson, our winning friends would still help us out.
But in retirement planning, people do not share risk. The 95% winners have no obligation to bail out the 5% losers. This changes the game. This isn’t traditional ergodicity.
Instead, we’re all in the game by ourselves (like the time average participant), but only have one shot to get it right (lest our retirement plan fail). From the ergodicity point of view, it’s a conundrum. It’s like playing Russian Roulette with a 20-chamber gun (5% failure = 1 chance in 20).
How do potential retirees react to this change in the rules?
For starters, many real retirement plans are couched with so much conservatism that the retiree ends up with more money when they die than when they retired. Put another way—their investment gains outpace their ability to spend.
And we know that money is time. Therefore, we can conclude that many people work for years more than they need to. They’re cursing at spreadsheets when they could be sipping mojitos. Pardon my 2020 vernacular, but this is an abundance of caution.
Is there an ergodic solution to this over-cautious planning?
Does Ergodicity Have a Solution?
What did we learn from Mike Tyson ergodicity example? What did we learn from our coin flipping?
If we share risk, we reduce our potential upside but also eliminate downside.
Imagine that 100 retirees pool a portion of their money together. They all know that 95% of them won’t need to dip into that pool. They also know that their money in the pool is probably going to have worse returns than it would outside of that pool.
However! These 100 retirees also realize that the pool will save 5 of them from failure. And thus, the pool guarantees that their retirement will be successful. Instead of 100% of them worrying about a 5% downside, now none of them need to be concerned.
The purpose of investing is not to simply optimise returns and make yourself rich. The purpose is not to die poor.
William Bernstein
Some of you will know that this “pool” concept already exists. It’s called an annuity.
Annuities?! Jesse, You Son of a B…
Wait, wait, don’t shoot me! Besides, you only have one bullet in those 20 chambers (thank ergodicity)
Real quick: an annuity is a financial product where a customer pays a lump sum upfront in return for a series of payments over the rest of their life. Insurance companies often sell annuities.
Annuities—on average—are losing propositions. Just like my pool above, the average annuitant will suffer via opportunity costs. Their money—on average—is better invested elsewhere.
Insurance protects wealth. It doesn’t build wealth.
Ben Carlson
Never let someone convince you that an insurance product is going to build your wealth. Why? There are only two parties involved—you and the insurance company. If you’re building wealth, then the insurance company is…losing money? No way.
Insurance products are equivalent to average mutual funs with high fees. The high fees drain you like a vampire bat. They make money, and you lose via opportunity costs.
But one thing that annuities get right is that they hedge against downside risk in your retirement planning. The insurance company—i.e. my pool in the example above—collects a loss from most customers in order to provide a vital win to few customers.
This is just like real insurance. Most people pay more in insurance premiums—for their house, their car, their medical life—then they ever see in payouts. But for a vital few, insurance saves them from complete disaster.
Of course, detractors will rightly point out that annuities aren’t always guaranteed. If the insurance company goes belly-up, your state guarantor might only cover a portion of what you’re owed. Yes—that means your risk mitigation technique has risk itself. Riskception.
Annuities aren’t perfect. I don’t plan on buying one. But if the ergodicity of retirement planning has you fretting small chances of failure, annuities are one way to hedge that downside.
Is Robin Hood Ergodic?
Jesse is a boring index fund investor. It’s true.
But not Robin. She day-trades on Robin Hood, often experimenting with exotic trades with high leverage.
We can examine Jesse and Robin using ergodicity.
Jesse is playing the long game. In this simple hypothetical, his yearly returns are +30%, +10%, then -15%. The same three-year cycle keeps repeating. One might look at those three values and think, “Ah. About 8.3% per year, on average.”
Robin thinks daily. She wants money now. In this hypothetical, her daily returns are +60%, +15%, and -50%. The same three-day cycle keeps repeating. Again, one might look at those three values and think, “Ah. About 8.3% per day, on average.”
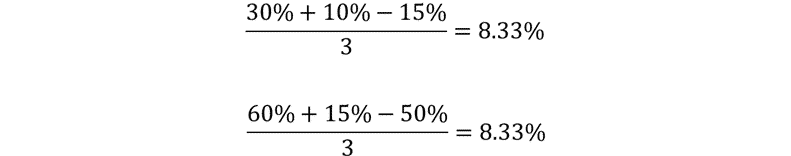
You might see a problem. We’ve used the arithmetic mean here. The arithmetic mean is useful in finding the expected value, in ergodicity terms. If Person A gains 60%, Person B gains 15%, and Person C loses 50%, their arithmetic average change is an 8% gain.
But sequencing investment returns—e.g. the ergodicity time average—requires that we use a log-average a.k.a. geometric mean. So let’s do that below:
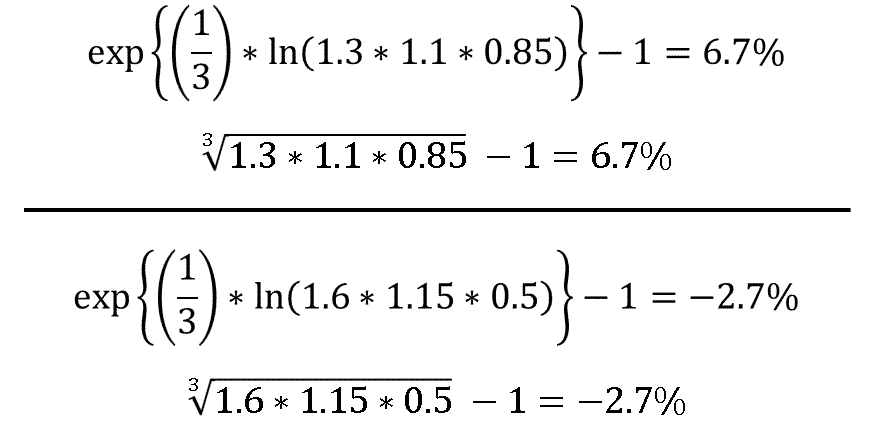
Thanks @pale_blue_dot for catching my original error
Uh oh. Robin’s log-average return is negative. And sure enough, if Robin executed this particular day-trading strategy, she would turn her $10,000 into $500 in less than four months. Meanwhile, Jesse is fine with his 6.7% annual return (trust me…he is).
In financial circles, the log-average of growth rates is known as the CAGR, or compound annual growth rate.
The simple lesson is one that new investors love to scream from the rooftops (and that’s a good thing). Namely, a given portfolio loss requires a larger equivalent gain to return back to even. The arithmetic mean does not capture this fact, while the log-average does.
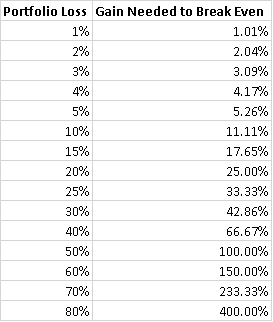
The larger the loss, the more significant the returning gain needs to be. That’s another ergodicity concept.
E.g. a 1% loss is offset by a 1.01% gain—they’re essentially the same. But a 50% loss—like the one Robin suffers every third day—requires a 100% gain to offset it
Just like we said earlier in the post—big risks matter most, and those large downsides are when we’re likely to see non-ergodic systems.
Everyday Ergodicity
I would argue that a smooth, ergodic personal life is also optimal. Imagine ranking your days on a scale of 1-10. Would you rather have half 10’s and half 4s? Or all dependable 7’s? Or two-thirds 10’s and one-third 1’s?
To each their own. I’d prefer the 7’s. I don’t want half my days to be “bad,” even if the flip side of that coin is that half my days are “perfect.”
Don’t make ‘perfect’ the enemy of good enough.
-Someone at Jesse’ work
Maybe it’s boring. Maybe it’s the same muscle that pushes me towards indexing and away from Gamestop. To each their own. But I’ll take the 7’s.
Ergodicity in Grad School
In grad school, I studied fluid dynamics. See—this is me! Specifically, I worked on reaction-diffusion-advection problems in the University of Rochester Mixing Lab.
Fluid mixing is a terrific example of ergodicity. Take a few seconds to watch the video below. It’s an aesthetic way to view equilibrium statistic physics. Ergodicity applies to many different dynamical systems, stochastic processes, thermodynamic equilibrium problems, etc. It’s a mechanical engineer’s dream.
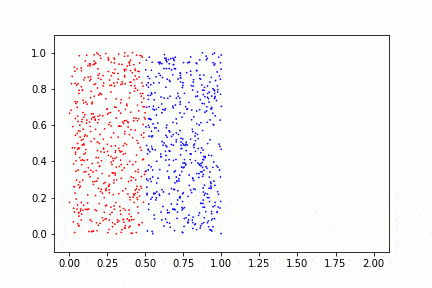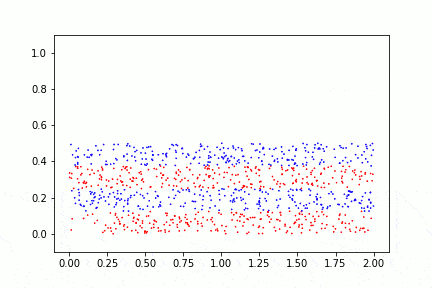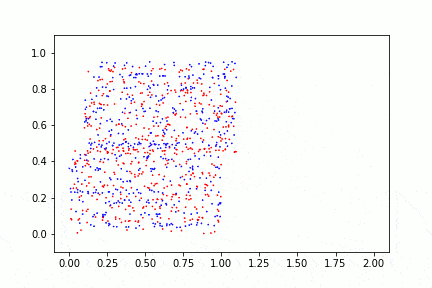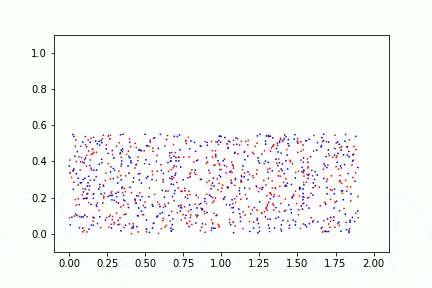
If we mix sufficiently, we see that small sub-sections of the fluid are representative of the fluid as a whole. The time average of many mixes is equal to our expected value of a uniform mix. This is ergodicity. This system is ergodic.
If this was butter and sugar—soon to be cookies—we could take any teaspoon of the mixture and draw reasonable assumptions about the mixture as a whole. Mmmmm!
But imagine if we accidentally introduce a dog hair into the mix (not that that’s ever happened in my kitchen). Suddenly, the mix is no longer ergodic.
Why? The expected value of any given cookie is that it will not contain the dog hair. But of course, eat enough of the cookies and you’ll eventually find the hair.
Or put another way, a single teaspoon of the mixture—which will contain either the entire dog hair or no dog hair at all—is no longer representative of the total mixture.
Good Article. Ergo…
Ergo it’s time for the summary.
Ergodicity is a fun concept. Or at least fun for nerds like me. It’s a terrific way to consider risk. It helps us in behavioral economics, personal finance, and real retirement planning.
What do you think? Any cool ergodic or non-ergodic systems in your life?
Thank you for reading! If you enjoyed this article, join 8000+ subscribers who read my 2-minute weekly email, where I send you links to the smartest financial content I find online every week.
-Jesse
Want to learn more about The Best Interest’s back story? Read here.
Looking for a great personal finance book, podcast, or other recommendation? Check out my favorites.
Was this post worth sharing? Click the buttons below to share!
Thanks for my new word of the day! (Actually two Ergodic, Non-Ergodic)
I saw the foreshadowing of the annuity coming. Really liked your Don’t shoot he messenger comment right afterwards, you were reading my mind.
Great Blog post really enjoy reading them.
Thanks for my new word of the day! (Actually two Ergodic, Non-Ergodic)
I saw the foreshadowing of the annuity coming. Really liked your Don’t shoot he messenger comment right afterwards, you were reading my mind.
Great Blog post really enjoy reading them.
Hey Tech.
Thanks a bunch! I’m happy to have you here reading 🙂
All the best,
Jesse
I have never heard about ergodicity.
Until now!
Hi Jesse,
Thanks for this interesting and fun article on ergodicity.
I will read the rest of your blog as i expect the same level of quality and fun…. hopefully this is an ergodic process… 😉
Hey CoolFox! Thanks for reading, glad you enjoyed it! I hope the rest of the blog lives up to these standards 🙂
I think you’ll find as you go deep into the Archives that my writing has improved (probably in a non-linear fashion, haha).
Cheers,
Jesse
Thanks for a well-written, informative, and thought-provoking article on a useful concept. I had to take the math on faith, but the ideas still came through clearly.
Hi AJ, thank you for the kind words. I really appreciate that comment.
All the best,
Jesse
Finally! A clear explanation of ergodicity! And non-ergodic processes! I’d heard the term but couldn’t find anything comprehensible about it.
Who knew non-ergodic processes line up with an unnamed concept I already have?
I signed up for your newsletter. I want more great stuff like this. It’s an order of magnitude better than the even the good personal finance blogs I’ve seen elsewhere.
Thanks so much, JTE 🙂
I really appreciate your kind words, and I’m glad the article resonated with you!
Jesse,
I‘ve been reading you for the past 4 weeks or so and enjoying many of your articles. But this one, found via a link in the recent one (about not dying with millions in the bank), really hit the ball out of the park for me. I deal with some pretty nerdy stats in my professional life, but I had never heard of ergodicity. Truly enlightening. And thx for a few good laughs along the way as well!
Richie
Hi Richie…that’s amazing 🙂
Thank you for reading and for the kind words.